スクリュー・プロペラへの挑戦
スクリュー・プロペラの設計。最初はそんなに難しいとは思っていなかった。アルミの板をひねって、簡単に作れると思っていた。しかし、どうやらそんなに簡単なものではなく、きちんと考えて作らなければダメだとわかった。
簡単に作ったものではなぜだめなのか? 各部の形状による水の抵抗を排除し、ブレードの角度と発生させる水流の速度を、勘ではなくて計算に基づいて設計しなければならないからだ。そのことに、何段階かの思考実験を経て気づいた。
まずはこんなモノを想像してみた。
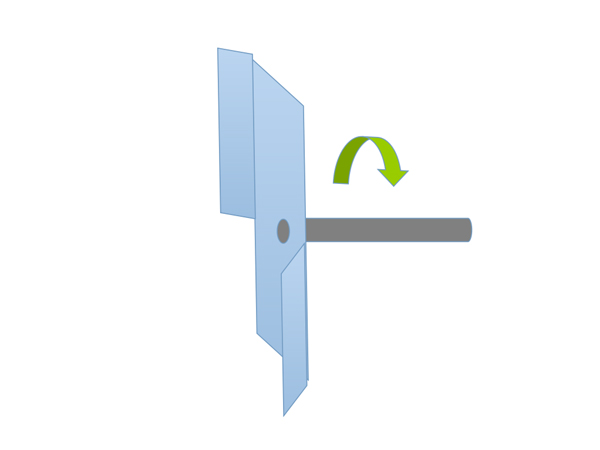
これは単純にアルミの板を曲げたものである。しかし一見して、角度を持たない平面部が、ボートの進行に対して大きな抵抗となることがわかる。これではダメだ。
では、次のようなモデルはどうか? シンプルにブレードのみで構成されており、中央のバーは抵抗とはならない。

このモデルがダメなのは、発生する水流に強弱の差が生じることだ。プロペラの中心部と周辺部とでは、ブレード断面の運動の速度が異なる。回転とは、円の中心に対して一定の角度変化で継続する、円運動である。中心からの距離によって、回転の角度は一定でも、ブレードの運動速度は異なる。その結果、プロペラ周辺部では強い水流が発生し、中心部では弱い水流が発生する。
とすると、ボートの速度が上がって、プロペラ中心部の水流速度を上回った場合、働いているのはプロペラ周辺部のみで、中心部は単なる抵抗となるということだ。そのようなプロペラは効率的ではない。
では、ブレードの中心部と周辺部で、異なる角度を持つようにできないか? 例えば、1枚のアルミの板を、左右から反対方向にひねって。
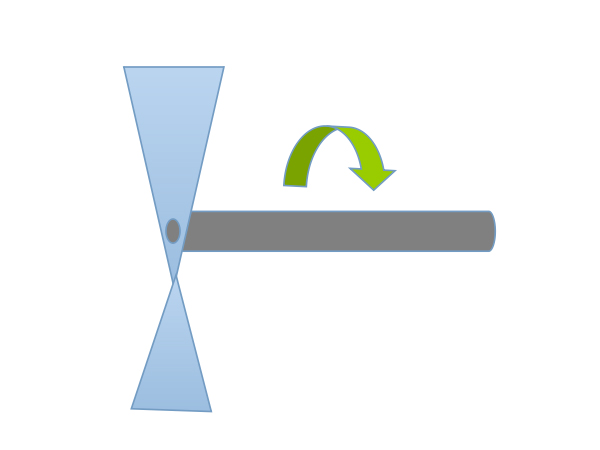
上のイメージはダメだ。角度の変化が逆だ。中心部の角度が寝ており、周辺部の角度が立っている。これではますます発生する水流の速度差が大きくなる。シャフトへの取り付け方を間違えている。ブレード面を回転方向に水平に取り付けるのではなく、垂直に取り付けるのだ。
正解は次のようなモデルだ。
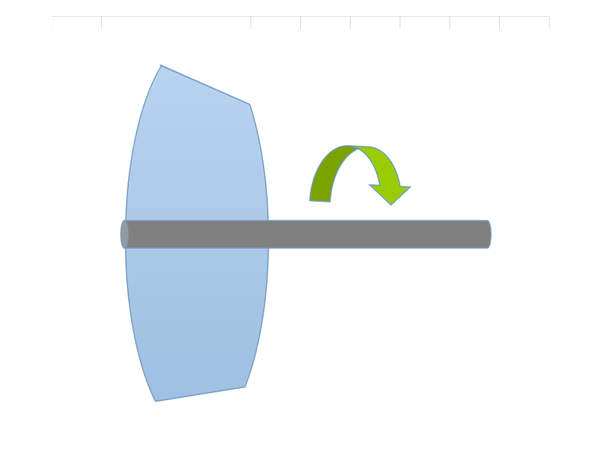
これだと、ブレード中心部の角度が立っており、周辺部の角度が寝ている。この角度の差によって、ブレードの回転速度差を相殺し、ブレードの全域で同じ速度の水流を発生させることができる。
しかし、問題が2つ生じる。
1)万力か何かを使い、手作業でひねって、適切なブレードの角度変化をうまく実現できるのか?
2)私の腕力でひねることのできる厚さのアルミの板で作ったブレードなら、何かにぶつかって衝撃を受けたりした時、強度が足りなくて容易に歪んでしまうのではないか?
だから、1枚のアルミ板をひねってスクリュー・プロペラを作るというアイデアは放棄しなければならない。
答えはらせん階段
中心部と周辺部で等速の水流を発生させるための、ブレードの角度変化のコントロール。どのような法則性を頼りに答えを見つければよいのか? そんなふうに考えても、私の数学力では答えを見つけることなどできない。きっと微分やら積分やらが必要なのではないのか?
だから、もっと別の発想法で答えに迫ることにしよう。プロペラを回転させて考えるから難しいのだ。逆の発想をしてみよう。プロペラが回転するのではなく、水が回転するのだ。するとひらめいた。プロペラをらせん階段に、水を人に置き換えて考えればいい。
らせん階段を、何人かが横一列になって上ってゆく。横一列を維持しようとするなら、内側の人はゆっくり、外側の人は速く前に進んでいかなければならない。それでも階段を上る段数は同じなのだ。これをプロペラに戻して考えてみる。らせん階段のようなプロペラが回れば、発生する水流の速度は、プロペラの中心部でも周辺部でも等速である。これが答えだ。

この方法なら、ブレードの角度変化を適切にコントロールできる。いったんはらせん階段を作っておいて、後で角を落として滑らかにすればいいのだ。そのような方法でプロペラを作ることができるのではないか?
ヒントを得て、一気に飛躍する設計
スクリュー・プロペラはらせん階段をヒントとして、積層の方法で作ることができることはわかった。では次の課題として、ブレードの傾きをどのように設計すればよいのか、考えてみることにする。
作るべきスクリュー・プロペラは、時速何kmの性能を目標とするのか。これがカギを握る。ここはひとつ思いっきり大げさに問題を立ててみよう。世界で一番速い海流に逆らって進むことのできる性能を持たせるなら、それはいったい時速何kmなのか?
この問題を調べてみて、意外なことが分かった。答えはなんと黒潮だ。最高で時速8km。したがって私の作るボートは時速8km以上の速度が出なければならない。そうでないと、何かのアクシデントに見舞われたとき、ハワイまで流されてしまうことになる。べつに黒潮本流までカツオを釣りに行くわけではないんだけどね。
ボートの最高速度が時速8km以上だとすると、それを実現するスクリュー・プロペラは、時速何kmの水流を発生させなければならないか? スクリュー・プロペラの発生させるエネルギーは、船体の抵抗によっていくらか減衰されるだろう。どれくらい? 私にはそれに答えるだけの経験がない。あてずっぽうで、水流の速度の3分の1と考えることにしよう。つまり、ボートを時速8kmで航行させようとするなら、スクリュー・プロペラは時速12kmの水流を発生させなければならないということだ。
では、時速12kmの水流を発生させるためには、どのようにスクリュー・プロペラを設計しなければならないのか? すでに固定されている数値がある。
1)ブレードの材料は、長さ30cm、厚さ3mmのアルミの板だ。したがってスクリュー・プロペラの直径は30cmということになる。
2)プロペラを回すべべルギアは、ギア比4:1を予定している。すなわちペダル1回転で、スクリュー・プロペラは4回転する。
仮に、最大限に漕いで、1秒にペダルを2回転させるのが限界だとしよう。この設定で時速12kmの水流を発生させればいいのだ。
では、ブレードの角度は何度にすればいいのか? それはこう考えればいい。
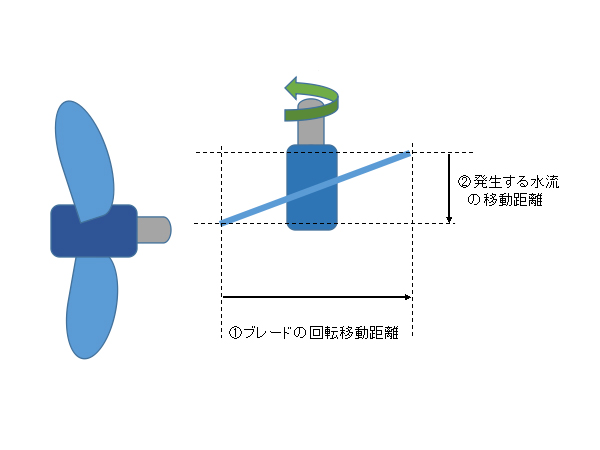
まずは1秒あたりのブレードの移動距離を求めよう。
ブレードの直径30cm×円周率3.14×ペダル1回転あたりプロペラ4回転×1秒間にペダル2回転=753.6cm
次に、目標の時速12kmを秒速に換算しよう。
12km×100,000cm÷60分÷60秒=秒速333.3cm
ではこの比率を求めよう。
333.3cm÷753.6cm=0.442
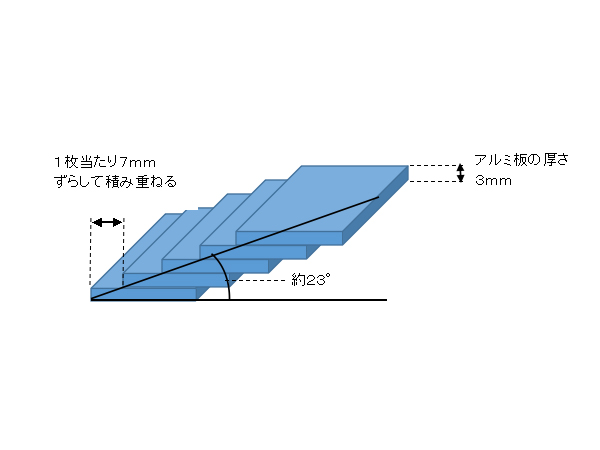
これは三角関数だ。たぶんタンジェントだったはず。タンジェントの値が0.442となるのは何度? その答えは約23°だ。ブレードの最も外周部での角度である。しかし、分度器で測って作業するわけではない。厚さ3mm、長さ300mm、幅25mmのアルミ板を、少しずつずらして積み重ねる。では、1枚当たり何mmずつずらして積み重ねれば、その傾きが23°になるだろうか?
3mm÷比率0.442=6.79mm
外周部でのアルミ板のずれは約7mmだ。これで、これから取り組むべき作業が見えてきた。
非力なプロペラと強力なプロペラの選択
ところで、アルミ板を積み重ねる枚数はどうすればよいだろうか? 手元には24枚分の材料があるのだが。
たくさん積み重ねれば積み重ねるほど、分厚いスクリュープロペラになる。スクリュー・プロペラの、進行方向に対する長さ(厚さ)は、ブレードの幅を意味する。この要素は、発生させる水流の初速には影響しない。これによって決定するのは、一度に動かす水流の水量だ。ブレードの幅が狭く、発生する水流の水量が少なければ、結果として水流はすぐに弱まり、速度が落ちるかもしれない。ブレードの幅が広ければ広いほど、強力なスクリュー・プロペラとなる。
スクリュー・プロペラのパワーは、ペダルをこぐ力に跳ね返る。どちらのプロペラを選ぶべきか?
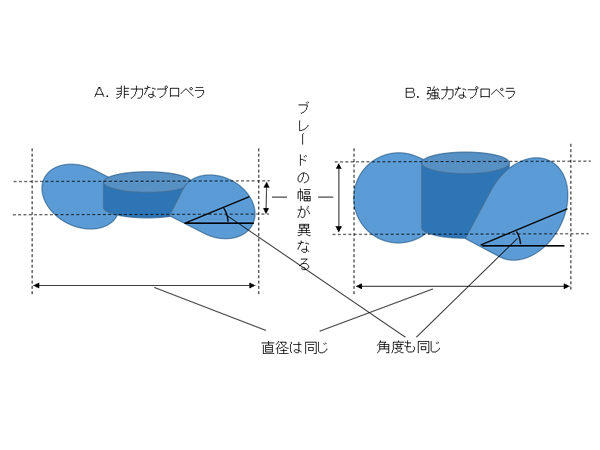
Aの非力なプロペラは、発生させる水流の水量が少ないため、漕ぐ力が少なくて済む。したがってペダルの回転は軽くて速いが、速く漕いでも加速はゆっくりで、じわじわとしか加速しない。
かたやBのプロペラは、発生させる水流の水量が多いため、漕ぐ力は多く必要となる。したがってペダルの回転は重くて、よほど力を込めて漕がない限り、速く漕ぐことができない。そのため、やはり加速はじわじわと効く。しかし脚に負担をかけて力強く漕げば、それに比例して強力な加速を得ることも可能だ。
両方とも、脚にかかる力が同じであれば、同じ加速をするだろう。その場合、Aは最初から速くペダルをこぎ始めてますます速く漕ぐようになり、Bはゆっくり漕ぎ始めて徐々に速くなる。要するに、Aのプロペラは高回転型で、Bのプロペラは高トルク型なのだ。
ボートの速度が上がれば上がるほど、両方とも、ペダルの重さは逓減する。最初からペダルの軽いAの場合はますます軽くなり、Bの場合は程よく軽くなって速く漕げるようになる。
どちらのプロペラを選ぶべきか? いざというとき、たとえ足に負担はかかっても、強力な加速ができる方がいいのではないか? 例えば漁船や貨物船を避けて急に進路を変更し、相手の進路から逃げなければならないようなときに。したがって、答えはBだ。用意した24枚分のアルミ板は全部使って、幅の広いブレードを作ることにする。
これで設計は完成した。これより実際の作業工程に突入する。
