等速往復運動
カーディナルのオシレーションを、改造によって、完璧な等速往復運動を行うようにしたい。しかも、ウォームシャフト方式ではなく、よりシンプルなクランク方式によって。
私はダイワの「S字カム」によって、そのヒントを得た。(ところで、あのパーツの名称は「カム」でいいのか?)。カムの形状によって、コサインカーブを描く運動を補正して、等速往復運動を実現することは、おそらく可能なのだ。ただし相当知恵を絞らなければなるまい。
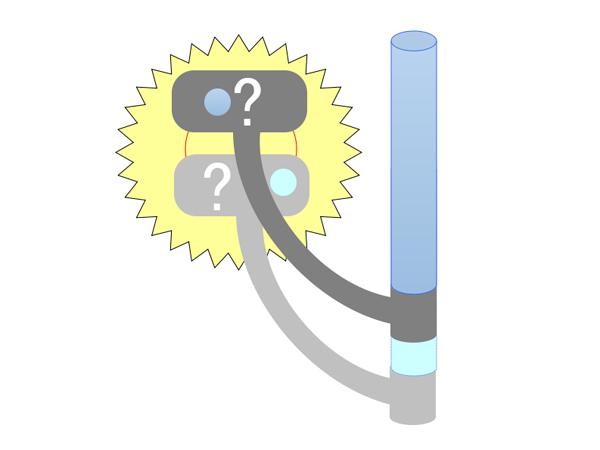
問題は上図の「?」の箇所の形状なのだ。これをどのように設計すればよいのだろう?
当然、このカムの機能には回転子の強制的な横スライドを含むので、カム自身が左右に振れてはいけない。だからコンロッドの振り子運動は排除し、固定されたつっかえ棒として、カムとスプールシャフトを一定の角度でつなぐだけのものとなる。
カムは縦方向には動いて、スプールシャフトを上下させなければならないが、横方向には回転子の動きをスライドによって逃がすと同時に、何らかの形状を持った斜面によって縦方向の往復運動の速度を等速に補正しなければならない。そのような形状は一体どのようなものか?
無限カムの着想
数週間考えて、私はアプローチの方法を見つけた。理屈で考えるから難しくなる。そうではなくて、実験してみればいいのだ。ただし、思考実験を。
このようなアプローチの仕方を何と呼べばいいのかわからない。背理法? それとも演繹法? あるいは帰納法? とにかく、すでに完璧な等速往復運動を実現しているものという前提で、あるべきカムの形状を、クランク運動に描いてもらえばいいのだ。「あなたはどのようなカムの形状を望んでいるの?」と。
それが下の図である。
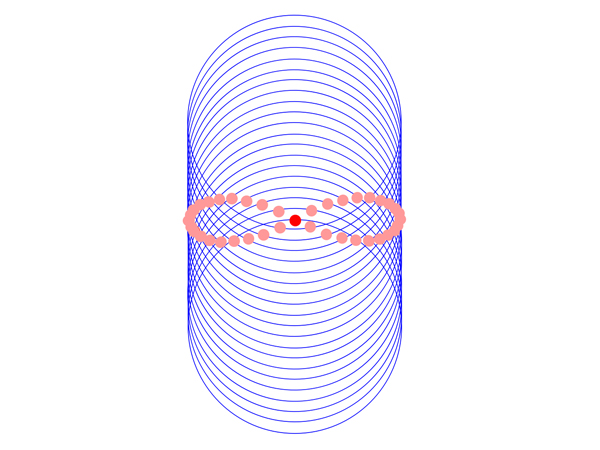
スプールシャフトが上下するとわかりにくい。カムが移動するので、2次元に図形を描けない。だからスプールシャフトが固定、したがってカムも固定、ドライブギアが往復運動をするものとして、相対的に逆転させて考えてみた。
ドライブギアの1周を40等分した。描画の間隔は角度にして9度だ。9度ごとのドライブギアの回転に連れて、そのドライブギアが等速で均等に移動する。このときカムとして求められる形状は、上図のとおり「∞」型である。これが答えだ。白紙のカムに、いわば回転子がこの形状を描いてくれたのである。(あのポッチの呼び名は「回転子」でいいのか?)。
等速往復運動のシミュレーション
念のため、今度は逆方向のシミュレーションをしてみよう。「∞」型のカムがいかなるメカニズムでスプールシャフトを等速往復運動させるのか。
上の動画は、ギア1周当たり40枚の画像に分解して、それを連続的につなげたアニメーションだ。アニメーションの精度が低く、フレームの設定が悪くて、まるでギアが反時計回りに回転しているように見えるが、実際には時計回りだ。
しかし、「∞」型のカムがクランク運動を補正して、等速往復運動を実現していることは十分に確認できる。このことにより、私は答えを得た。カムは「∞」型で行く。
問題の発生
工作が難しいなとは思う。しかしやってみれば、できないことはないだろう。私はわくわく、うきうきした。これは面白いことになるぞ。
しかし2、3日ののち、私はあることに気付いた。このカム、真ん中の交差した箇所で、回転子は期待通りに動いてくれるのだろうか? 交差して反対側へ迷い込んだりはしないだろうか?
いや、ありうる。回転子(動画で水色の点)が真ん中へ来たとき、回転子は斜め上に進むのか、斜め下に進むのか、どちらかいっぽうに確定されていない。どちらにも進みうる。
いや、それだけではない。左右の両端でも、回転子はさらに進むのか、折り返して戻るのか、一方に確定されていない。外的な力が加われば、期待通りではない動きをする可能性がある。外的な力とは、例えばスプールに働く地球の引力だ。
心臓と血流に例えると、何か弁のような役割を果たすものが必要なのだ。そうでなければ血液は予期せぬ流れ方をして、正しい機能を果たせない。
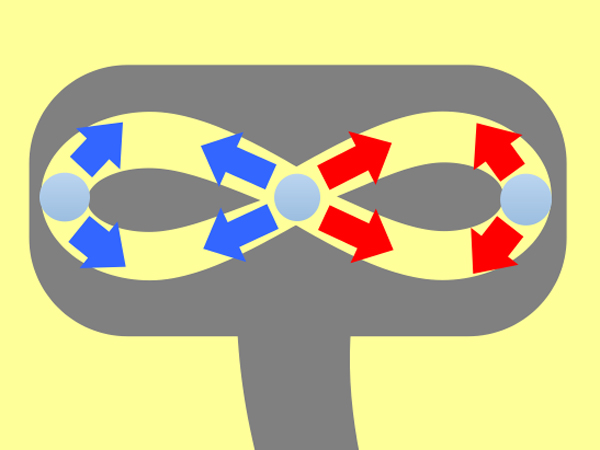
さて、この問題をどうする?
